ANN: Mathematical Model

Mathematical Model of an ANN

Each neuron computes a weighted sum of its inputs, adds a bias term, and applies an activation function. The output of a neuron can be represented as:

\[ y = f\left( \sum_{i=1}^{n} w_i x_i + b \right) \]

where ( w_i ) are the weights, ( x_i ) are the inputs, ( b ) is the bias, and ( f ) is the activation function.

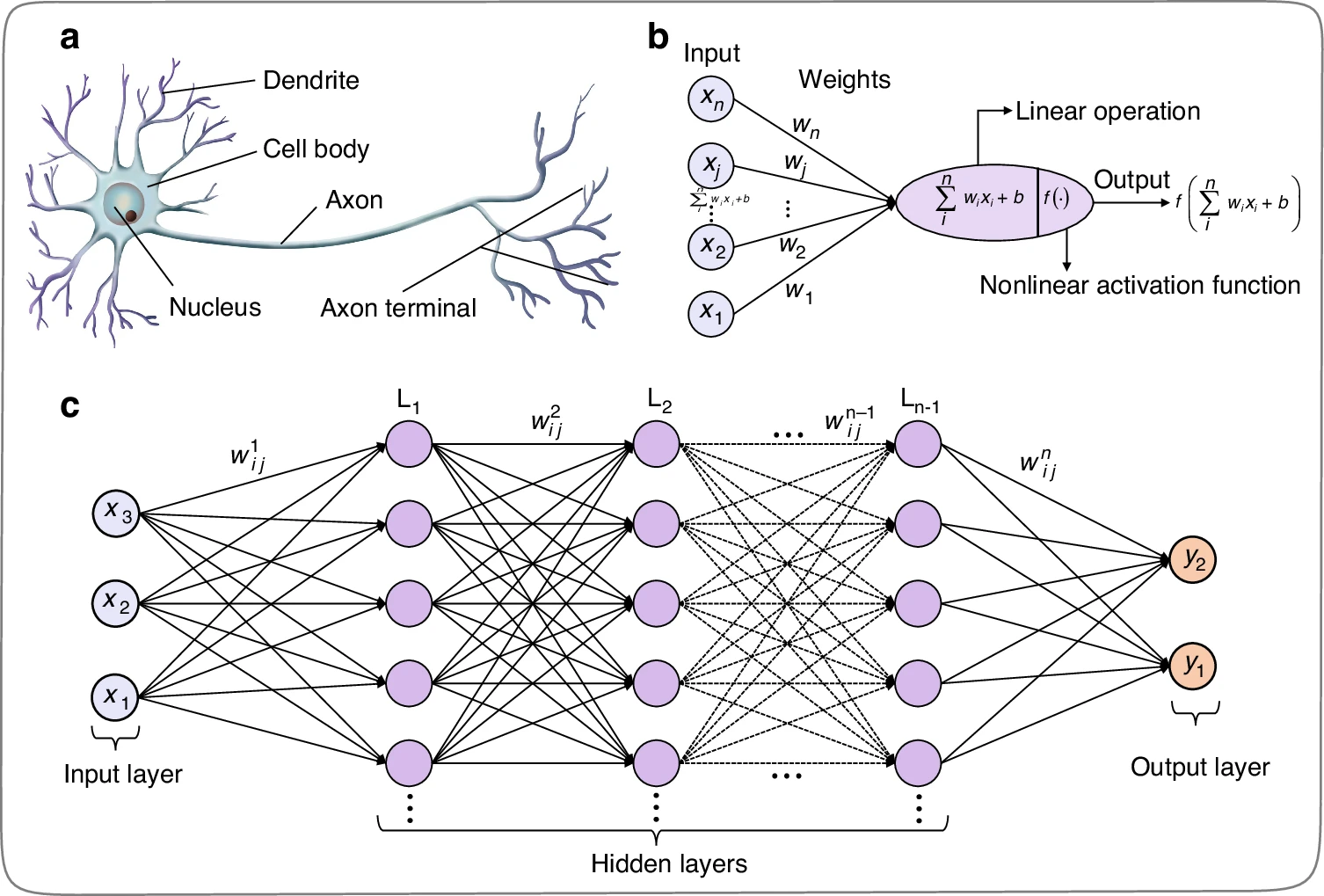
From: Optical neural networks: progress and challenges

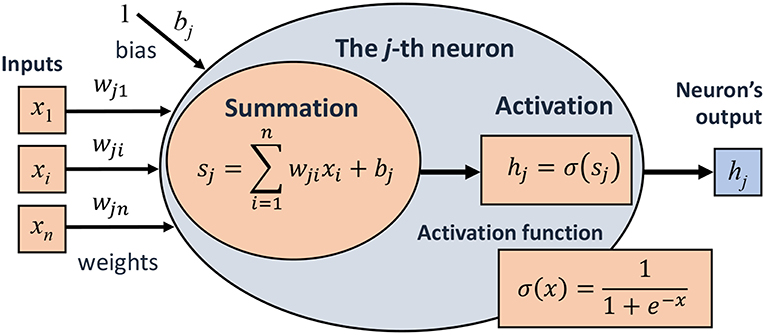
Neuron structure and artificial neural network. a Structure of biological neurons. b Mathematical inferring process of artificial neurons in multi-layer perceptron, including the input, weights, summation, activation function, and output. c Multi-layer perceptron artificial neural network

Structure of Biological Neurons

A biological neuron consists of three main components: dendrites, soma, and axon[2]. Dendrites receive input signals from other neurons. The soma, or cell body, contains the nucleus and processes information. The axon transmits signals to other neurons through synapses[2][8].

An artificial neuron in a multi-layer perceptron (MLP) mimics the biological neuron’s function:

Inputs: Represented as a vector [1] \[x = [x_1, x_2, ..., x_n]\]
Weights: Each input is associated with a weight [1] \[w_i\]
Summation: The neuron computes a weighted sum of inputs:

\[v = \sum_{i=1}^n w_i x_i + b\]

where \[b\] is the bias term[1].
Activation Function: The sum is passed through an activation function \[f\]

\[y = f(v)\]

Common activation functions include sigmoid, hyperbolic tangent, and ReLU[1][10].
Output: The result \[y\] is the neuron’s output[1].

Multi-layer Perceptron Neural Network

An MLP consists of multiple layers of interconnected neurons:

Input Layer: Receives the initial data[3].
Hidden Layers: Process information through weighted connections and activation functions[3].
Output Layer: Produces the final result[3].

The network learns by adjusting weights and biases through backpropagation, minimizing a cost function[4][9]. This process allows the MLP to model complex relationships between inputs and outputs, making it suitable for various machine learning tasks[3][9].

Citations: